Page affichée à 07:45:37
samedi 27 juillet 2024
Ce site n'utilise pas de cookie.Dôme acoustique Compteur pour tout le site : 14 871 808
Nombre actuel de lecteurs : 93.Faire
un don
par
PayPalLe site de Dominique, un amateur passionné
2-3-1-3 : Formules de calcul des pavillons
Mise à jour : 03 février 2023, Antidote 11.
Préambule :
L'homme a toujours su naturellement exploiter la fonction de porte-voix simplement en plaçant ses mains devant la bouche.
De la même façon, on peut augmenter le rendu acoustique d'un haut-parleur en le chargeant avec un pavillon.Le pavillon acoustique joue le rôle d'un transformateur acoustique entre la haute impédance de la source rayonnante (en l'occurrence la membrane du haut-parleur, dont la masse volumique est forte, par exemple le papier utilisé pour la fabrication des cônes) et la très basse impédance acoustique de l'air dont la masse volumique est faible (1,18 kg/m3).
Il est en effet démontré physiquement qu'il est toujours très difficile de transmettre une vibration d'un milieu dense à un milieu léger.Lors du fonctionnement dynamique du haut-parleur, le pavillon a pour effet physique d'augmenter la masse volumique apparente de l'air au voisinage du cône : il s'ensuit une meilleure transmission des vibrations.
On trouve dans la littérature beaucoup de publications qui s'intéressent aux pavillons acoustiques.
Certains des livres publiés sont très théoriques et il est difficile aux néophytes d'en extraire la substantifique moelle et de passer ainsi à une réalisation pratique.
D'autres ouvrages se présentent comme des articles scientifiques, mais ne donnent en fait que des recettes mystérieuses et secrètes, sans aucune base technique sérieuse, ce qui est toujours un peu frustrant.
Dans tous les cas il manque toujours une ou deux données essentielles pour pouvoir enfin ( ! ) concevoir et réaliser un pavillon acoustique.Dans une forme que nous espérons la plus claire et concise possible, cet article n'a que pour modeste ambition d'établir les bases et principes nécessaires à la réalisation pratique des pavillons acoustiques.
Ce chapitre est basé sur un grand nombre d'équations pas toujours facile à comprendre pour certains.
Il est associé à un autre chapitre, les pavillons pour les nuls, chapitre qui explique exactement les mêmes choses, mais sans la moindre équation.
Définitions :
Surface de gorge Sg : c'est la surface à l'entrée du pavillon.
Cette surface peut être très faible dans le cas des pavillons pour compression, par exemple 5.07 cm2 pour un pavillon pour moteur de 1" de diamètre 2.54 cm.Surface de bouche Sb : c'est la surface de la sortie du pavillon.
La surface minimale, pour rayonner correctement une fréquence, dépend de la longueur d'onde.Moteur : c'est la chambre de compression, généralement pour médium ou aigu, qui contient la membrane et l'aimant.
L'association {pavillon + chambre de compression} se comporte comme un filtre passe-bande.
En effet, le pavillon ne transmet correctement que les fréquences supérieures à une fréquence de coupure basse que nous appellerons Fcb.
Cette fréquence de coupure basse est liée à la forme géométrique du pavillon.
La chambre de compression agit comme un filtre passe-haut pour les fréquences qui sont supérieures à une fréquence de coupure haute que nous appellerons Fch.
Cette fréquence est directement liée aux dimensions géométriques de la chambre de compression.
Schéma de principe :
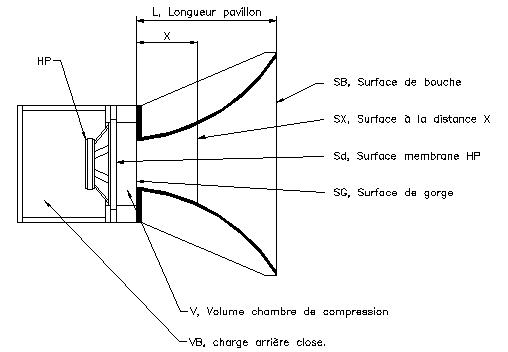
Le schéma ci-dessus est le plus général possible, il montre un haut-parleur chargé par un pavillon, une chambre de compression, une charge arrière.
Si la charge arrière peut être un autre pavillon, un volume clos, une enceinte Bass reflex, un baffle plan, une enceinte infinie, rien, le plus courant est un volume clos.
Le schéma est applicable à la reproduction des sons graves, médiums et aigus, car les formules d'expansion sont uniques et universelles.
Rendement d'un pavillon :
Le calcul de la sensibilité se fait dans le cas d'un pavillon de grave, ou de bas médium, qui utilise un haut-parleur de 10 à 46 cm de diamètre.
Dans le cas d'un pavillon de médium aigu, le fabricant du moteur donne directement la sensibilité en fonction du pavillon utilisé.
Calcul de la surface de la gorge Sg par L'Audiophile numéro 11 de juillet 1979 :Soit Aopt, le rapport entre Sg et Sd, ou
- Sg est la surface de gorge du pavillon, et
- Sd la surface de la membrane du haut-parleur utilisé.
Les unités sont en m2.
Rendement théorique maximum :
Aopt = Re / ( Re + ( BL2 / 2 / Ro / C / Sd ) ) avec :
Ro = 1.200 kg/m3 à 40% Hr
C = 343.4 m/s à 20° Celsius
Re = Résistance au courant continu de la bobine du haut-parleur en Ohms
BL = Facteur de force en N/A
Sd = Surface de la membrane du haut-parleur utilisé en m2.Sg = Aopt * Sd
Rendement réel :
Connaissant Aopt calculé ci-dessus, ou A = Sg / Sd si Sg n'est pas optimum, il est possible de calculer le rendement théorique du haut-parleur avec son pavillon :
Rend% = BL2 * Re * A / ( Ro * C * Sd * ( Re + A * ( Re + BL2 / 2 / Ro / C / Sd ) )2 ) * 100.Il est facile de convertir le rendement % en sensibilité en dB/2.83V/m par la formule :
Sensibilité = 10 * LOG( Rend% / 100 ) + 112.13 en dB.Le rendement varie assez peu en fonction de la variation de Sg.
La longueur totale du pavillon sera d'autant plus courte que Sg sera grand.Pour un pavillon de grave, vous avez donc tout intérêt à retenir un Sg supérieur au Sg qui donne le rendement maximum.
J'ai peu d'expérience sur les pavillons avant pour haut-parleur.
Mais le peu d'essais que j'ai fait confirme que la surface de gorge qui donne les meilleurs résultats d'écoute est pour A > Aopt, avec 0.8 < A < 1.
Ce n'est pas une règle absolue, c'est une piste qui a pour base deux essais avec deux haut-parleurs différents.La surface de gorge est utilisée dans le calcul des différentes surfaces en fonction de la longueur avec une loi d'expansion.
Autre formule :
Y.ROCARD dans son livre "Dynamique générale des vibrations" aborde le sujet et explicite par un calcul approché, l'amplification apportée par un pavillon.
Cette amplification théorique A est telle que :
( Sb / 2 * Sg )0,5 < A < ( Sb / Sg )0,5
Ce qui donne, traduit en dB, les formules :
5 * LN ( Sb / 2 * Sg ) < A dB < 5 * LN ( Sb / Sg ).Sg = 2 * pi * Fs * Qts * Vas / C
Fs, Qts, et Vas sont les paramètres électromécanique du Haut-parleur, C = 343.4 m/s, pi = 3.14159.
En pratique :
Carré intégralement contenu dans un diamètre de surface Sd :
Pour un bon couplage avec le haut-parleur, je prends une surface de gorge carrée, dont la diagonale est égale au diamètre émissif de la membrane : Sg = 0.64 * SM.
C'est plus grand que la surface qui donne la sensibilité maximum, et ce n'est pas trop petit pour ne pas avoir un pavillon trop long.
Diamètre du haut-parleur = Diam = racine( Sg x 4 / pi )
Côté du carré = Diam / racine( 2 )Carré de surface 0.9 x Sd :
J'ai très peu réalisé de pavillon.
À l'écoute, il semblerait qu'une surface de gorge égale à 0.9 fois la surface de la membrane donne les meilleurs résultats à l'écoute, au prix d'une perte de sensibilité sans doute inacceptable en sono.
Sg = 0.9 * Sd.Carré de surface Sd :
Si vous sacrifiez un peu plus de rendement et de sensibilité, pour gagner sensiblement en longueur du pavillon.
Bonne formule pour un pavillon rond équipé d'un large bande qui monte dans le médium.Carré contenant intégralement un diamètre de surface Sd :
Si vous ne voulez pas cacher le moindre cm2 de la membrane active, en gardant une gorge carrée plus facile à réaliser.
Vous avez accepté de perdre en rendement et sensibilité.
Diamètre du haut-parleur = Diam = racine( Sg x 4 / pi )
Côté du carré = DiamDans le cas des pavillons arrière, la surface de gorge est inférieure à la surface de gorge qui donne le rendement et la sensibilité maximale.
Volume clos arrière :
Pour avoir la sensibilité calculée, le volume à l'arrière du haut-parleur doit être clos, pour renvoyer dans le pavillon toute l'énergie sonore.
Le haut-parleur, dans ce volume clos, voit sa fréquence de résonance qui remonte.Calcul de cette fréquence de résonance :
- Fs = Fréquence de résonance du haut-parleur à l'air libre.
- Vas = Volume d'air équivalent à l'élasticité de la suspension en L.
- Qts = Coefficient de surtension totale du haut-parleur.
- Fc = Fréquence de résonance du haut-parleur dans le volume clos.
- Vb = volume du volume clos en L.Qtc = Qts * racine ( ( Vas / Vb ) + 1 )
Fc = Qtc / Qts * Fs
Fc = Fs * racine ( ( Vas / Vb ) + 1 ).Fc fixe le milieu de la bande passante en puissance reproduite par le pavillon.
La largeur de la bande passante, par rapport à Fc, est donné par le Qts du haut-parleur retenu.
Autre formule :
Le volume de charge arrière du haut-parleur, doit être d'après KLIPSH, tel que :
Vb = C * Sb / ( 2 * pi * Fc ).
Je n'ai pas évalué cette formule, j'ai juste vérifié la cohérence des unités.
Elle me semblerait plus plausible sous la forme Vb = C * Sg / ( 2 * PI * Fc ), ce n'est qu'un avis...
D'autre part, comme Fc dépend directement de Vb, nous sommes dans le cas du serpent qui se mort la queue !!!Voir aussi : http://melhuish.org/audio/horn.html
Idéalement :
La distinction entre les fréquences de coupure haute en réponse et en puissance m'a été précisée par J. Fourcade.
Le calcul utilise la fréquence de coupure haute en puissance.Le volume clos doit être choisi pour que Fc soit le milieu de la bande passante en puissance qui correspond à votre besoin.
Soit Fcb votre limite basse, et Fchp votre limite haute en puissance, le milieu Fcc = racine( Fcb * Fchp ).
Par exemple avec 70 et 450 Hz, le milieu est à 177.5 Hz et non pas à 260 Hz : les échelles sont logarithmiques sur les fréquences.
Une fréquence de coupure de 450 Hz en puissance correspond environ à une fréquence de coupure de 450 * 2.8284 = 1270 Hz en réponse.
Cette valeur de 1270 Hz doit être vérifiée avec le logiciel de simulation des pavillons Hornresp.Il convient de vérifier que la bande passante souhaitée est compatible avec la bande passante théorique que peut donner le haut-parleur.
Voir Bande passante théorique ci-dessous.Avec la fréquence centrale Fcc, et les paramètres du haut-parleur Fs et Vas, vous pouvez avoir directement le volume clos à utiliser :
Vb = Vas / ( ( Fcc / Fs )2 - 1 ).
Une erreur grossière :
J'ai vu certain d'entre vous calculer le volume clos pour que Fc soit plus bas que la fréquence basse dont ils avaient besoin.
Une enceinte à pavillon n'est pas une enceinte close, même s'il y a aussi un volume clos dont la Fc se calcule comme pour une enceinte close.
Le volume clos d'un pavillon n'est là que pour renvoyer l'énergie dans le pavillon.
Les coupures acoustiques d'une enceinte à pavillon sont données par le Qts du haut-parleur, la taille et la loi d'expansion du pavillon.
Bande passante souhaitée :
La distinction entre les fréquences de coupure haute en réponse et en puissance m'a été précisée par J. Fourcade.
Cette bande passante est définie par les deux fréquences extrêmes, la fréquence de coupure basse Fcb et la fréquence de coupure haute en réponse Fch.
Nous allons définir une autre fréquence de coupure haute en puissance, Fchp, qui est définie avec Fch / 2 ou Fch /4.Dans les outils de calculs, je vais calculer trois cas, avec un espacement constant étant donné que les échelles en fréquences sont logarithmiques :
- Fchp2 = Fch / 2
- Fchp3 = Fch / 2 / racine( 2 ) = Fch / 2.8284
- Fchp4 = Fch / 4
Bande passante théorique :
Une fois la fréquence Fc (ou Fcc) du volume arrière du pavillon connue, une fois le Qts du haut-parleur connu, la bande passante du pavillon est assez simple à calculer.
Définissons Fcb_th comme la fréquence de coupure basse théorique du pavillon, et Fch_th comme la fréquence de coupure haute théorique.
Nous avons, Fcb < Fc < Fch.
- Fcb_th = Fc / 2 / Qts * [ racine( 4 * Qts2 + 1 ) - 1 ]
- Fch_th = Fc / 2 / Qts * [ racine( 4 * Qts2 + 1 ) + 1 ]
D'après le livre Audio de Mario ROSSI, chapitre 9.4.4, pages 616 et 617.
Nous pouvons calculer la bande passante en puissance à partir des valeurs théoriques de Mario ROSSI.
Comme pour la bande passante souhaitée, nous aurons là aussi trois valeurs qui me semblent plus pertinentes que celles calculées avec la bande passante souhaitée.Choisissons un volume clos tel que Fcc = 150 Hz.
- Pour un haut-parleur avec un Qts = 0.125, Fcb_th = 18.4 Hz, Fch_th = 1220 Hz.
- Pour un haut-parleur avec un Qts = 0.250, Fcb_th = 35.4 Hz, Fch_th = 636 Hz.
- Pour un haut-parleur avec un Qts = 0.500, Fcb_th = 62.1 Hz, Fch_th = 362 Hz.
- Pour un haut-parleur avec un Qts = 0.810, Fcb_th = 83.3 Hz, Fch_th = 269 Hz.
Un volume clos avec une Fc = 150 Hz est un tout petit volume : il sera choisi la plupart du temps un volume plus grand qui donne une Fc plus faible.
La conséquence est un déplacement de la bande passante vers le grave, et une limite de la bande passante dans le médium.
La bande passante ne sera pas utilisée dans le grave, l'encombrement du pavillon est trop important.
La limite de la bande passante dans le médium sera a prendre en compte.
Enfin, si vous voulez monter un peu dans le médium, choisissez un haut-parleur avec un Qts très faible.Il y a des réalisations avec un volume arrière beaucoup plus grand, volume accordé en Bass reflex.
Considérons ce volume clos, et regardons, sur un exemple, la conséquence sur la bande passante.
Prenons l'ALTEC 515C avec un Qts de 0.166.
- Avec un volume arrière de 50.5 L, Fb = 13.9 Hz, Fh = 530 Hz.
- Avec un volume arrière de 150 L, Fb = 8.7 Hz, Fh = 332 Hz.La formule d'expansion du pavillon sera calculée pour une fréquence bien inférieure à Fc, et compatible avec la bande passante pratique souhaitée dans le grave.
Il existe aussi les formules de Don KEELE, qui sont utilisées dans la documentation JBL en PDF :
Flc = Fs * Qts / 2. Beaucoup trop bas pour être d'une quelconque utilité.
Fhm = 2 * Fs / Qts. Début de la pente à 6 dB/octave.
Fhvc = Re / pi / Le. Début de la pente à 12 dB/octave.
Haut-parleurs adaptés aux pavillons :
Si vous avez besoin de bande passante dans le médium, ce sont obligatoirement des haut-parleurs avec un Qts très faible qui conviennent.
Plus le Qts sera faible, plus la bande passante sera grande, si on s'en tient aux équations de Mario ROSSI.Il n'est pas précisé que cette bande passante n'est vraie que s'il y a une chambre de compression entre le haut-parleur et le pavillon.
Il y a de nombreux exemples de pavillon dont la surface de gorge est égale à la surface de la membrane.
Équipés de haut-parleurs large bande, l'ensemble monte jusqu'a l'aigu.
Le plus souvent, ces larges bandes ont aussi un Qts faible.La recherche multicritères pour pavillon de la base de données permet de trouver les hauts-parleurs les mieux adaptés à cet usage.
Les critères sont le Qts, la sensibilité en pavillon et la fréquence de coupure haute d'après ROSSI.
Les paramètres de calculs sont la surface de gorge et le volume clos à l'arrière du haut-parleur.
Les autres paramètres de calcul sont la résistance du filtre passif, le facteur d'amortissement de l'ampli, le nombre, montage et branchement des haut-parleurs.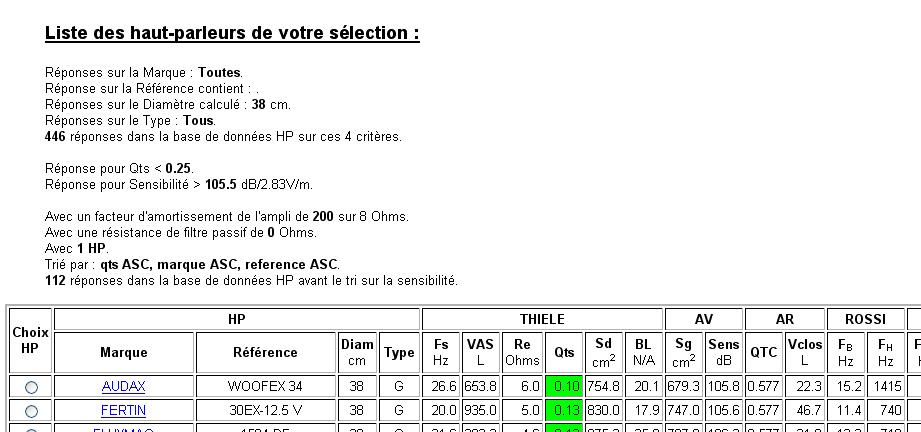
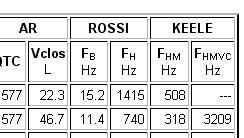
Cette recherche propose 16 haut-parleurs parmi les 446 possibles sur les 4 premiers critères.
C'est une recherche particulièrement pertinente, et exactement adaptée à votre cas.
Si votre demande est possible, la recherche multicritères vous trouvera votre haut-parleur idéal...
Formules d'expansion :
Il y a 4 types de pavillon :
- Le pavillon hyperbolique.
- Le pavillon exponentiel.
- Le pavillon TRACTRIX.
- Le pavillon BESSEL.
Ces pavillons utilisent un coefficient M et pour les pavillons hyperboliques, un coefficient T.
Le coefficient M :
Calcul du coefficient d'expansion M :
M = 4 * pi * Fexp / C, avec :
- Fexp = Fréquence de coupure théorique du pavillon.
- C = 343.4 m/s à 20°C
- pi = 3.14159.
Pour Fexp = 1000 Hz, M = 4 * pi * 1000 / 344 = 36.530 m-1.
Pour Fexp = 250 Hz, M = 4 * pi * 250 / 344 = 9.133 m-1.Attention, la valeur de Fcb doit être corrigée.
Dans le cas d'un pavillon exponentiel, il faut faire le calcul à une fréquence 2.500 fois plus faible que celle souhaitée en pratique Fcb.
Si vous souhaitez une coupure Fcb = 1500 Hz, calculez-le pour Fexp = 1500 / 2.500 = 600 Hz.
M = 4 * pi * 600 / 344 = 21.918 m-1.Dans le cas d'un pavillon hyperbolique avec T = 0.707, il faut faire le calcul a une fréquence 1.500 fois plus faible que celle souhaitée en pratique.
Si vous souhaitez une coupure à Fcb = 1500 Hz, calculez-le pour Fexp = 1500 / 1.500 = 1000 Hz.
M = 4 * pi * 1000 / 344 = 36.530 m-1.Pour T > 1.000, je garde le coefficient 2.500.
Pour T < 0.707, je garde le coefficient 1.500.
Pour les valeurs entre T = 1.000 et T = 0.707, je fais une interpolation linéaire Cefficient = a * T + B.
Le coefficient T :
Valeur de T :
- Si T = 1.000, pavillon exponentiel.
- Si T = 0.707, pavillon hyperbolique théorique idéal.
- Si T < 0.707, ce que l'on gagne en fréquence de coupure est perdu par le risque résonance vers la fréquence de coupure, sauf si le but est d'annuler la réactance acoustique sans modifier la surface de gorge.
Pavillon hyperbolique :
La formule de l'expansion d'un pavillon hyperbolique est :
- S = Sg * ( COSH ( M * X / 2 ) + T * SINH ( M * X / 2 ) )2
OU :
Pour pouvoir le calculer en PHP qui n'a pas les fonctions COSH et SINH.
Calculs en 3 lignes, pour simplifier l'écriture et le nombre de parenthèses.
- eq_cosh = ( EXP ( M * X /2 ) + EXP ( -M * X / 2 ) ) / 2
eq_sinh = ( EXP ( M * X / 2 ) - EXP ( -M * X / 2 ) ) / 2
S = Sg * ( eq_cosh + T * eq_sinh )2Avec :
- S = Surface en cm2 à la distance X.
- Sg = Surface de départ, de gorge, en cm2 à la distance X = 0 en m.
- X = Distance entre la surface S et la surface Sg en m.
- COSH = Cosinus hyperbolique = ( EXP ( M * X ) + EXP ( -M * X ) ) / 2.
- SINH = Sinus hyperbolique = ( EXP ( M * X ) - EXP ( -M * X ) ) / 2.
- M = Coefficient d'expansion lié à la fréquence en m-1.
- T est un coefficient qui modifie la forme et la vitesse d'expansion.
- EXP = Exponentielle.
J'ai vérifié dans EXCEL, avec T = 0.707 et T = 1, M calculé pour 100 Hz, Sg = 120 cm2 et C = 343.707 m/s, pour des longueurs entre 0.0 et 125.0 cm :
- eq_cosh avec COSH.
- eq_sinh avec SINH.
- S = Sg * ( eq_cosh + T * eq_sinh )2 avec S = Sg * ( COSH ( M * X / 2 ) + T * SINH ( M * X / 2 ) )2.
La comparaison entre les calculs sous EXCEL, et ceux que je propose en PHP dans le site ne montrent aucune différence.
Pavillon exponentiel :
Avec T=1 et en simplifiant l'équation :
S = Sg * ( COSH ( M * X ) + 1 * SINH ( M * X ) )
S = Sg * ( ( EXP ( M * X ) + EXP ( -M * X ) ) / 2 + 1 * ( EXP ( M * X ) - EXP ( -M * X ) / 2 ) )
S = Sg * ( EXP ( M * X ) / 2 + EXP ( M * X ) / 2 + EXP ( -M * X ) / 2 - EXP ( -M * X ) / 2 )
S = Sg * ( 2 * EXP ( M * X ) / 2 )
S = Sg * EXP ( M * X ) , avec :
- S = Surface en cm2 à la distance X en m.
- SG = Surface de départ en cm2 à la distance X = 0 en m.
- X = Distance entre la surface S et la surface Sg en m.
- EXP = Exponentielle.
- M = Coefficient d'expansion lié à la fréquence en m-1.
Cette équation est beaucoup plus simple à manipuler que celle du pavillon hyperbolique, une simple calculatrice scientifique suffit.
La transformation des cosinus et sinus hyperbolique en exponentielle se trouve dans tous les formulaires de mathématique.
Pavillons TRACTRIX :
La formule utilisée est moins pratique à utiliser que les formules précédentes, car on donne d'abord la section du profil, ou son rayon pour le cas d'une trompe, pour atteindre X la distance comptée depuis la bouche (et non pas la gorge).
Le profil est similaire à ceux des pavillons exponentiels, mais avec une ouverture plus rapide quand on s'approche de la bouche (ce qui est d'ailleurs aussi le cas du fameux pavillon IWATA).
On calcule ces pavillons en utilisant la formule suivante, la fréquence de coupure basse est directement liée au rayon Rm de la bouche (voir deuxième formule):X = Rm * LN ( ( Rm + ( Rm2 - Rx2 )0.5 ) / Rx ) ) - ( Rm2 - Rx2 )0.5
Rm = C / 2 * pi * Fv
Avec :
- X = distance depuis la bouche en m.
- Rm le rayon du la bouche TRACTRIX
- Rx le rayon à une distance X de la bouche
NOTA : on fait les calculs facilement à partir d'un tableur.
Pour les valeurs de Rx supérieures à Rm, la formule n'est plus calculable, la valeur Rm2 - Rx2 dans le logarithme népérien étant négative.
Pavillons de BESSEL :
La formule utilisée est S = SG * ( M * X )b dont le pavillon conique avec b = 1, où encore les pavillons paraboliques avec b < 1, constituent des cas particuliers.
Peu intéressants en général.
Autre pavillon :
Il existe des expansions de pavillon, tel le pavillon IWATA, dont la forme d'expansion reste mystérieuse et souvent incomprise.
Il faut faire entrer une notion de plus, le report des surfaces calculées dans le plan.
Suivant que vous allez reporter des surfaces planes, cylindriques, sphériques, JMLC ou temporelles, vous n'aurez pas la même forme du pavillon en fonction du même calcul initial.
Le chapitre sur le report des surfaces vous explique la subtilité de passer du calcul au plan : si vous n'avez pas une bonne CAO, et le savoir-faire en dessin industriel, certains reports ne vous seront pas accessibles.Le pavillon IWATA, si vous l'étudiez avec des surfaces temporelles, il y a beaucoup moins de mystères, même si la loi d'expansion n'est pas "cassée " complètement.
À moins que ce soit des erreurs, volontaires ou pas, sur le plan initial...
Volume de la chambre de compression :
La chambre de compression et un petit volume entre la membrane et le début du pavillon.
Ce n'est pas le volume clos à l'arrière du haut-parleur ou de la compression.La chambre de compression se comporte comme un filtre passe-bas, avec une fréquence de coupure Fch.
Aussitôt que la longueur d'onde émise par le haut-parleur est voisine des dimensions de la chambre de compression, il y a une atténuation de l'onde transmise (réflexions : 6dB/octave).Le volume de la chambre de compression doit être en théorie tel que :
Vc = C * Sg / ( 2 * pi * Fch ) avec
Fch : fréquence de coupure haute.
Vc : volume de la chambre de compression.Le volume de la chambre de compression doit être (autre formule issue de la théorie) tel que :
E = C * Sg / ( 2 * pi * Fch * Sd ),
ceci lorsque la section de la chambre de compression est circulaire d'un diamètre égal à celui du haut-parleur (elle épouse donc la surface projetée d'émission de celui-ci).
E est simplement l'épaisseur pour une telle chambre de compression.Si nous prenons un haut-parleur de 30 cm avec Sd = 530 cm2
monté dans un pavillon avec Sg = 0.64 * SM = 338 cm2
pour monter dans le médium jusqu'a 1000 Hz
Vc = 1850 cm3 = 1.85 L
E = 3.5 cm.
La surface de bouche minimum :
Pour rayonner correctement une longueur d'onde, la circonférence à la surface de bouche doit être égale à la longueur d'onde.
C'est très facile pour les médiums et aigu, impossible ou très encombrant pour les graves...
Nous sommes dans le cas théorique ou N = 1, avec une diffusion dans l'espace dans 4 * pi stéradian.
Explication de rayonnement 4Pi, 2Pi, pi et pi/2 par True Audio.Pour les graves, utilisez le sol et deux murs (N = 8, pour un angle solide d'émission de pi / 2 stéradians) en plaçant le pavillon en encoignure comme pour une Klispchorn, c'est la seule solution "efficace"
Le pavillon vertical d'encoignure est une autre possibilité, à condition de tenir compte de la hauteur du plafond, et de faire la pièce de bois entre-le pavillon et le plafond.Les pavillons de graves de type "estrade", sont une alternative, avec N = 4 pour un angle solide d'émission de pi stéradian.
Vous trouverez sa description sur le forum Melaudia.
L'appui contre le mur latéral et le sol sont indispensables pour bien avoir un N = 4.Le tableau ci-après donne les valeurs de 16 à 5000 Hz, avec un échelonnement en 1/3 d'octave.
La célérité du son dans l'air est égale à 344 m/s.
N = 1 : Pavillon pour médium-aigu
complètement dégagé.N = 2 : Pavillon de graves
posé au sol et dégagé des murs
comme la plupart des SONO.N = 4 : Pavillon de graves
posé au sol et appuyé contre un mur.N = 8 : Pavillon de graves
posé au sol et dans l'angle de 2 murs
comme une Klispchorn !!!Fréquence Long. Onde Surface Diamètre coté du carré Surface Diamètre coté du carré Surface Diamètre coté du carré Surface Diamètre coté du carré 16 Hz 21.500 m 36.785 m2 6.844 m 6.065 m 18.392 m2 4.839 m 4.289 m 9.196 m2 3.422 m 3.033 m 4.598 m2 2.420 m 2.144 m 20 Hz 17.200 m 23.542 m2 5.475 m 4.852 m 11.771 m2 3.871 m 3.431 m 5.886 m2 2.737 m 2.426 m 2.943 m2 1.936 m 1.715 m 25 Hz 13.760 m 15.067 m2 4.380 m 3.882 m 7.534 m2 3.097 m 2.745 m 3.767 m2 2.190 m 1.941 m 1.883 m2 1.549 m 1.372 m 32 Hz 10.750 m 9.196 m2 3.422 m 3.033 m 4.598 m2 2.420 m 2.144 m 2.299 m2 1.711 m 1.516 m 1.150 m2 1.210 m 1.072 m 40 Hz 8.600 m 5.886 m2 2.737 m 2.426 m 2.943 m2 1.936 m 1.715 m 1.471 m2 1.369 m 1.213 m 7357 cm2 968 mm 858 mm 50 Hz 6.880 m 3.767 m2 2.190 m 1.941 m 1.883 m2 1.549 m 1.372 m 9417 cm2 1.095 m 970 mm 4708 cm2 774 mm 686 mm 63 Hz 5.460 m 2.373 m2 1.738 m 1.540 m 1.186 m2 1.229 m 1.089 m 5932 cm2 869 mm 770 mm 2966 cm2 615 mm 545 mm 80 Hz 4.300 m 1.471 m2 1.369 m 1.213 m 7357 cm2 968 mm 858 mm 3678 cm2 684 mm 607 mm 1839 cm2 484 mm 429 mm 100 Hz 3.440 m 9417 cm2 1.095 m 970 mm 4708 cm2 774 mm 686 mm 2354 cm2 547 mm 485 mm 125 Hz 2.752 m 6027 cm2 876 mm 776 mm 3013 cm2 619 mm 549 mm 1507 cm2 438 mm 388 mm 160 Hz 2.150 m 3678 cm2 684 mm 607 mm 1839 cm2 484 mm 429 mm 920 cm2 342 mm 303 mm 200 Hz 1.720 m 2354 cm2 547 mm 485 mm 1177 cm2 387 mm 343 mm 589 cm2 274 mm 243 mm 250 Hz 1.376 m 1507 cm2 438 mm 388 mm 753 cm2 310 mm 274 mm 320 Hz 1.075 m 920 cm2 342 mm 303 mm 460 cm2 242 mm 214 mm 400 Hz 860 mm 589 cm2 274 mm 243 mm 294 cm2 194 mm 172 mm 500 Hz 688 mm 377 cm2 219 mm 194 mm 188 cm2 155 mm 137 mm 630 Hz 546 mm 237 cm2 174 mm 154 mm 119 cm2 123 mm 109 mm 800 Hz 430 mm 147 cm2 137 mm 121 mm 74 cm2 97 mm 86 mm 1000 Hz 344 mm 94 cm2 109 mm 97 mm 1250 Hz 275 mm 60 cm2 88 mm 78 mm 1600 Hz 215 mm 37 cm2 68 mm 61 mm 2000 Hz 172 mm 24 cm2 55 mm 49 mm 2500 Hz 138 mm 15 cm2 44 mm 39 mm 3200 Hz 108 mm 9 cm2 34 mm 30 mm 4000 Hz 86 mm 6 cm2 27 mm 24 mm 5000 Hz 69 mm 4 cm2 22 mm 19 mm Si vous "piquez" mon tableau parce qu'il est "bien fait", laissez au moins mon nom --- Demandez l'accord et vous l'aurez --- Dominique PETOIN --- Dôme acoustique.
Formule de calculs :
C = 344 m/s.
Longueur d'onde = C / F.
Pour N = 1
Diamètre = Longueur d'onde / pi.
Surface_théorique = pi * Diamètre2 / 4.
Pour N = 1, 2, 4 ou 8.
Surface_pratique = Surface_théorique / N.
Diamètre = racine( Surface_pratique * 4 / pi ).
Côté du carré = racine( Surface_pratique ).La surface pratique est réduite de la surface théorique par un facteur N dont le coefficient est fonction de l'angle solide d'émission.
- N = 1 pour un diffusion dans l'espace ( Angle solide = 4 * pi ), pavillons pour médiums et aigus.
- N = 2 pour un diffusion frontale ( Angle solide = 2 * pi ), cas général des pavillons de graves posés au sol.
- N = 4 pour une diffusion posée au sol et appuyée contre un mur ( Angle solide = 1 * pi ).
- N = 8 pour une diffusion en encoignure avec le sol et 2 murs ( Angle solide = pi / 2 ).
Annuler la réactance du pavillon à la bouche :
Topt = 2 * pi * Fs / Fcb2 * Vas / Sg / C * 10
avec
Fcb = Fréquence de coupure basse souhaitée.
Fs = fréquence de résonance à l'air libre du haut-parleur. (Voir les T&S du haut-parleur).
Vas = Volume d'air équivalent à l'élasticité de la suspension en L, voir les T&S du haut-parleur.
Sg = surface de gorge en cm2.
10 est le résultat des 1/10000 pour passer de cm2 en m2, et des 1/1000 pour passer les L en m3, 10000 / 1000 = 10.
C = Célérité de l'air, environ 344 m/s.Si vous voulez faire un pavillon avec T = choisi, alors Sg = 2 * pi * Fs / Fcb2 * Vas / T / C * 10.
Calculs inversés :
Cette méthode de calcul est utilisée pour la vérification d'un pavillon existant, à partir des équations du pavillon exponentiel qui sont beaucoup plus simples dans ce cas.
Vous connaissez :
- La surface de sortie du pavillon, S en cm2.
- La surface d'entrée du pavillon, SG en cm2.
- La longueur du pavillon, X en m.
Calcul du coefficient M :
M = 1 / X * LOGN ( S / SG ), avec :
LOGN = Logarithme népérien, noté LN sur votre calculatrice.Exemple, un pavillon de médium avec SG = 4.9 cm2, S = 491 cm2, X = 0.2 m.
M = 1 / 0.2 * LOGN ( 491 / 4.9 ) = 23.036 m-1
Calcul de la fréquence F :
F = C * M / 4 / PI
Dans l'exemple ci-dessus, F = 344 * 23.036 / 4 / PI = 630.6 Hz.
En pratique cela fait un pavillon utilisable à 2.5 * 630.6 = 1500 Hz environ.
Vous connaissez :
- La surface de sortie du pavillon, S en cm2.
- La surface d'entrée du pavillon, SG en cm2.
- Le coefficient M.
Calcul de la longueur X :
X = 1 / M * LOGN ( S / SG ), avec :
LOGN = Logarithme népérien, noté LN sur votre calculatrice.Exemple, un pavillon de médium avec SG = 4.9 cm2, S = 41.85 cm2, M = 21.918 m-1.
X = 1 / 21.918 * LOGN ( 41.85 / 4.9 ) = 0.098 m = 9.8 cm.
Un cas parmi d'autres :
Imaginez que vous aviez conçu un pavillon hyperbolique avec T = 0.707, et que la simulation avec Hornresp vous montre que c'est idéal avec T = 1.000 :
Pour retoucher au minimum les plans, vous allez garder la surface de gorge SG, la surface de bouche S, la longueur totale X, et vous allez recalculer le pavillon avec un nouveau coefficient M, et une loi exponentielle.
Les formules ci-dessus vous disent comment calculer le nouveau coefficient M, la fonction "valeur cible" d'Excel vous évite tout calcul.Quelle est la différence de profil au milieu du pavillon ?
L'exemple prend pour base un pavillon hyperbolique T = 0.707, calculé à 60 Hz, avec SG = 1058 cm2 et une longueur de 93 cm.
Le pavillon exponentiel a une surface plus grande de 5% à la longueur de 60 cm. Il est calculé à 51.98 Hz.
Retoucher un plan sera facile.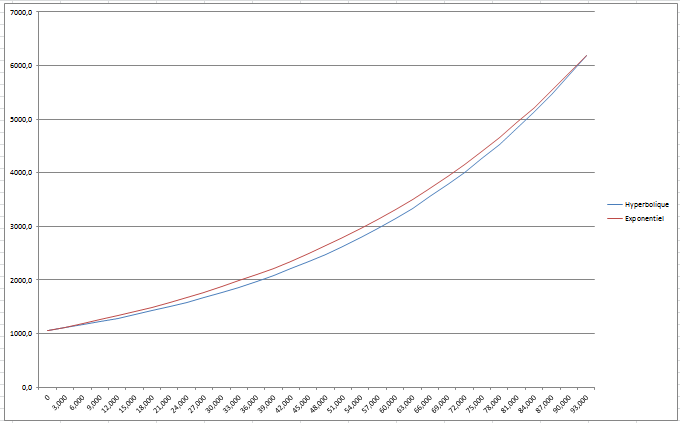
Et avec Hornresp ?
Hornresp est un logiciel de simulation des pavillons, dont les résultats m'ont sérieusement ébranlé, parce qu'ils ne sont pas en accord avec la partie précédente du chapitre.
Entre des théories plus ou moins justes, et une simulation avec un logiciel qui a fait ses preuves, la vérité est la simulation...
La mode d'emploi de Hornresp en téléchargement, parce qu'il ne faut pas le perdre, et qu'il est trop gros pour être affiché dans le chapitre.
Quelle valeur de T ?
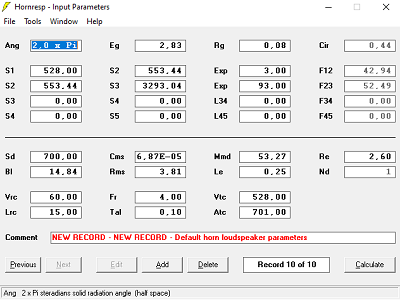
J'ai calculé 5 pavillons différents, même haut-parleur, même surface de gorge, même fréquence de calcul, même surface de bouche, mais avec 5 coefficients T différents.
Il y a deux haut-parleurs RCF MB 10G251, montés côte à côte et branchés en parallèle.
La surface de gorge est de 528 cm2, la loi d'expansion est calculée à 60 Hz avec T = 0.707, longueur du pavillon 96 cm, pas de calcul 3 cm.L'outil de calcul de la loi d'expansion est en bas de ce chapitre, pour les paramètres du haut-parleur équivalent il faut utiliser l'outil de calcul des pavillons avec :
1/4 - la référence contient : 10G251.
2/4 - cliquez dans le rond face au MB 10G251. Sélectionnez 2 HP montés côte à côte et branchés en parallèle.
3/4 - recopiez les valeurs ci-dessous.
4/4 - les T&S du haut-parleur équivalent, et le tableau avec les couples de valeurs (distance, surface).Les paramètres de départ avec des surfaces temporelles de la solution retenue sont :

Hypothèse pavillon infini, T=0.707 Hypothèse pavillon dans 2Pi stéradian, T=0.707 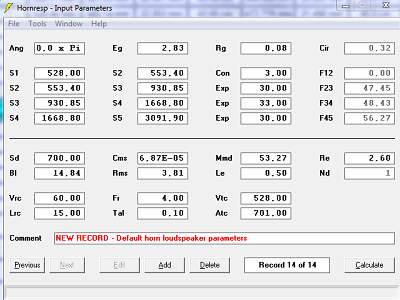
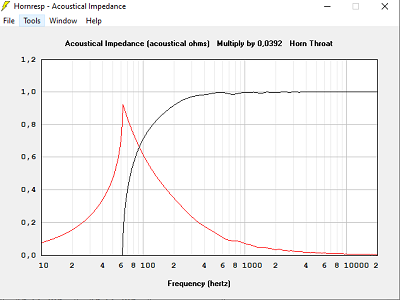
Hypothèse du pavillon infini :
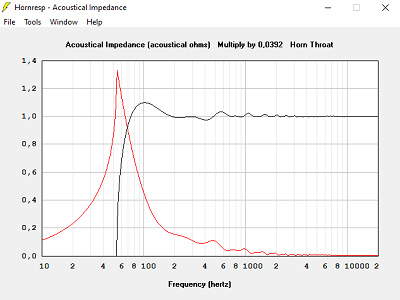
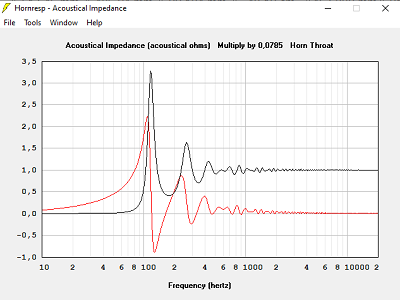
Avec T = 0.500, hypothèse pavillon infini 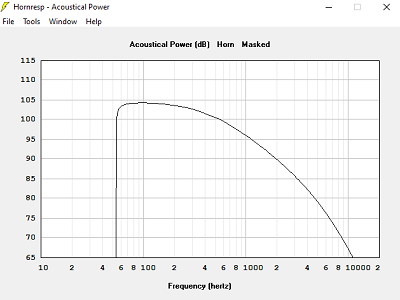
Avec T = 0.707, hypothèse pavillon infini 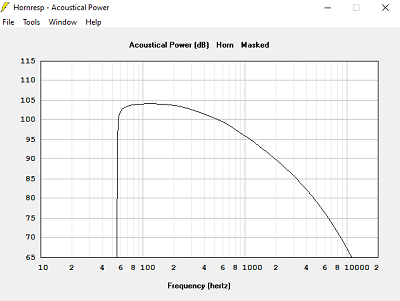
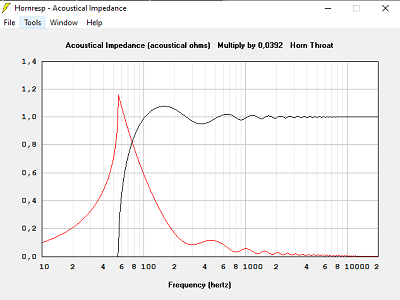
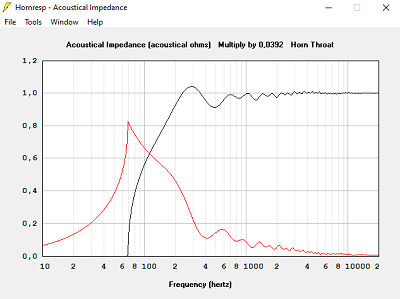
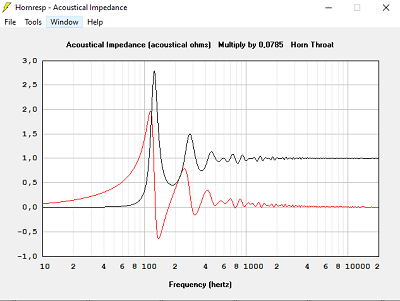
Avec T = 1.000, hypothèse pavillon infini, la meilleure solution, le pavillon exponentiel 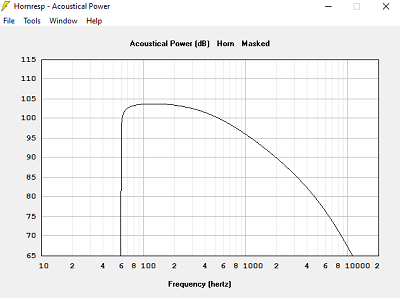
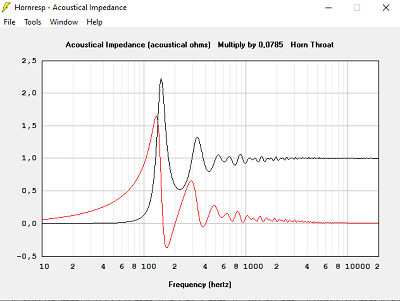
Avec T = 1.200, hypothèse pavillon infini 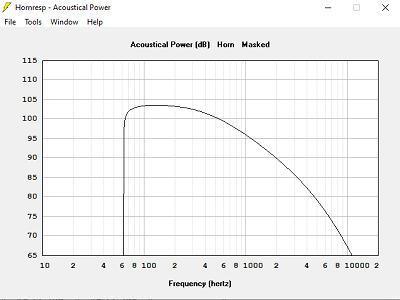
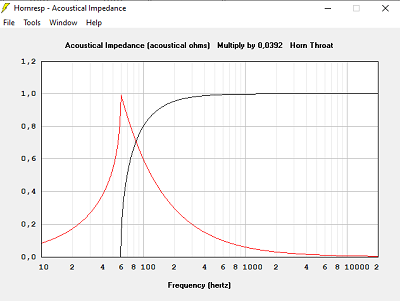
Avec T = 1.600, hypothèse pavillon infini 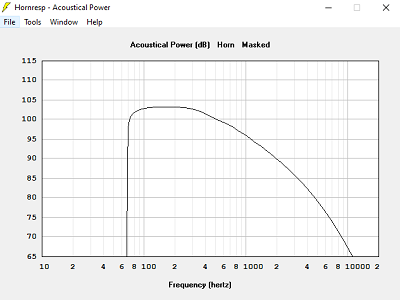
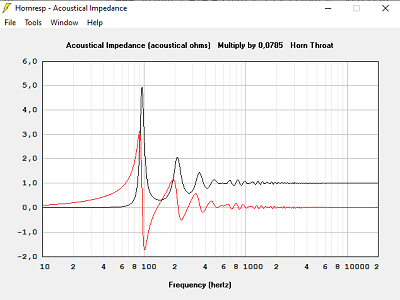
Hypothèse pavillon dans 2Pi stéradian :
Avec T = 0.500, hypothèse pavillon dans 2Pi stéradian 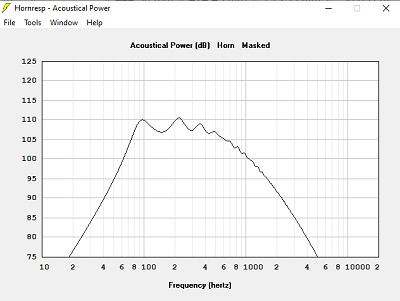
Avec T = 0.707, hypothèse pavillon dans 2Pi stéradian 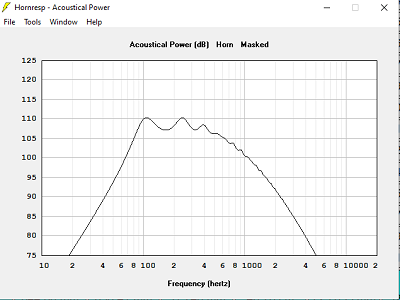
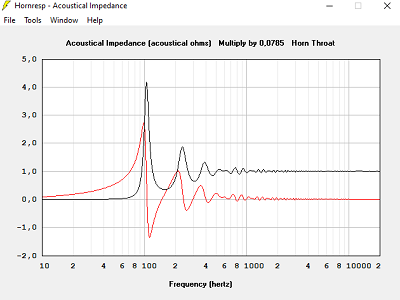
Avec T = 1.000, hypothèse pavillont dans 2Pi stéradian 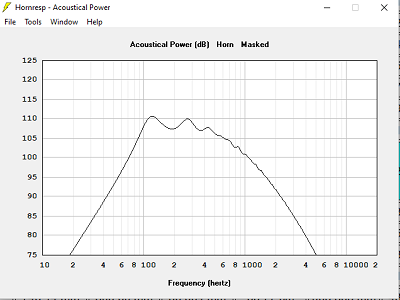
Avec T = 1.200, hypothèse pavillon dans 2Pi stéradian 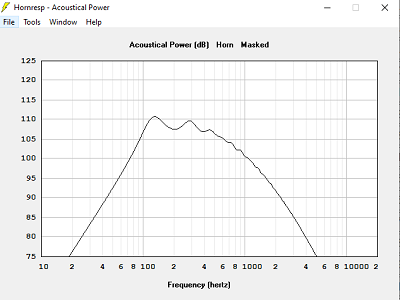
Avec T = 1.600, hypothèse pavillon dans 2Pi stéradian 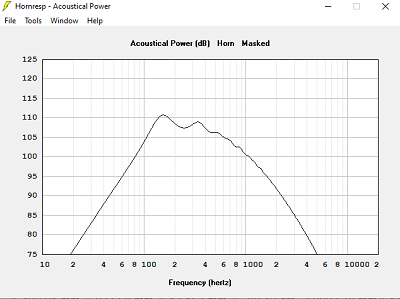
Je m'aperçois qu'avec Hornresp tous les pavillons descendent presque jusqu'à la fréquence de calcul, les coefficients 2.5 pour T > 1.000 et 1.5 pour T < 0.707 ne se vérifient pas.
Ce qui se vérifie bien, c'est une descente à 80 Hz à -1 dB pour un calcul à 60 Hz, environ 1.3 fois la fréquence de calcul.
Si on regarde les choses à -3 dB, c'est à peu de chose près la fréquence de calcul.La meilleure impédance acoustique est obtenue pour T = 1.000, ce qui conduit à une longueur de pavillon plus courte qu'avec T = 0.707 ou T = 0.500.
Je ne chercherai plus, je ferai des pavillons exponentiels avec T = 1.000, et avec la fréquence de coupure égale à 1.3 x la fréquence de calcul.Le T n'a aucune influence sur la fréquence de coupure en passe-bas, qui ne dépend que du Qts du haut-parleur, Qts qui doit rester aussi faible que possible si vous voulez monter dans le médium.
Quelle surface de bouche ?
J'ai calculé 4 pavillons différents, même haut-parleur, même surface de gorge, même fréquence de calcul, même coefficient T, 4 surfaces de bouche différentes.
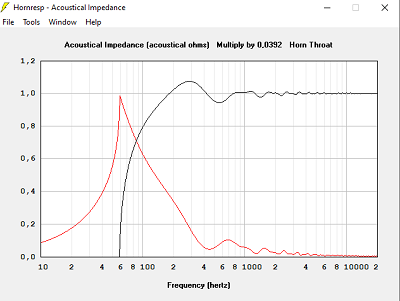
Avec Sb = 3694 cm2 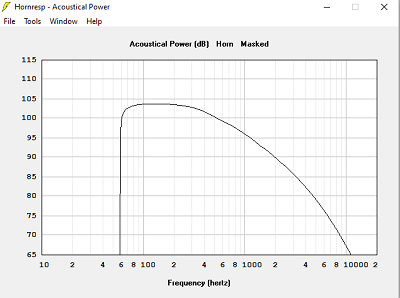
Avec Sb = 4501 cm2 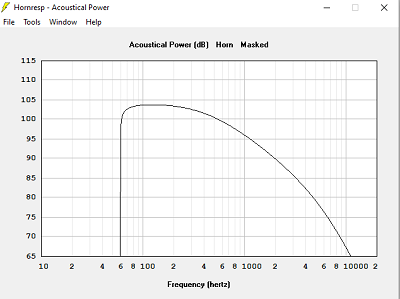
Avec Sb = 6254 cm2 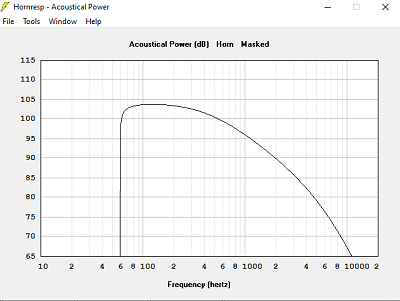
Avec Sb = 14714 cm2 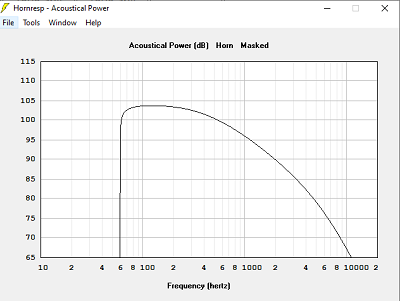
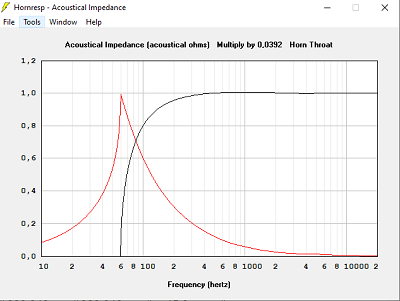
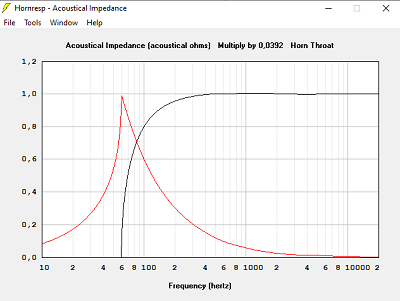
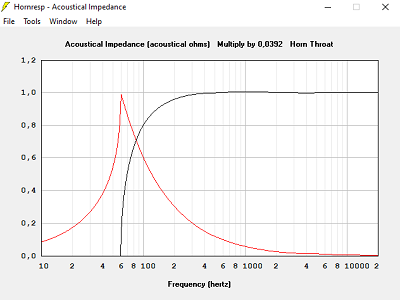
Un pavillon trop petit en surface est moins bon sur la courbe d'impédance acoustique.
Passé un seuil, augmenter la surface ce sert plus à rien.
La simulation avec Hornresp indiquera le seuil à chaque fois.
Quel volume clos ?
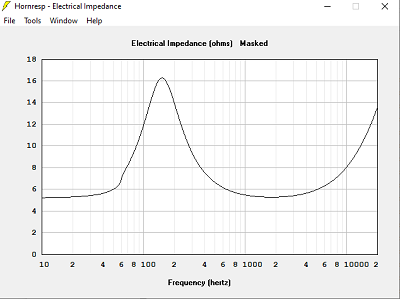
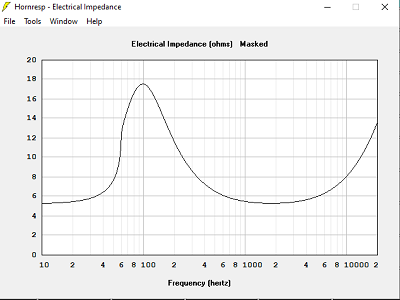
J'ai calculé 6 pavillons différents, même haut-parleur, même surface de gorge et de bouche, même fréquence de calcul, même coefficient T, avec différents volumes clos :
Avec Volume clos = 15 L 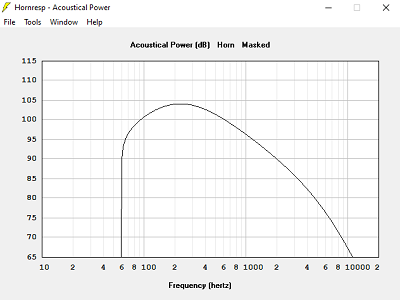
Avec Volume clos = 30 L 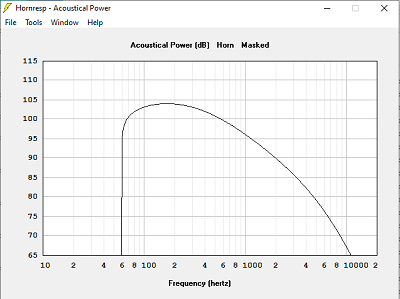
Avec Volume clos = 60 L 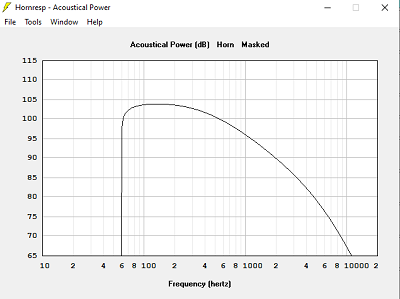
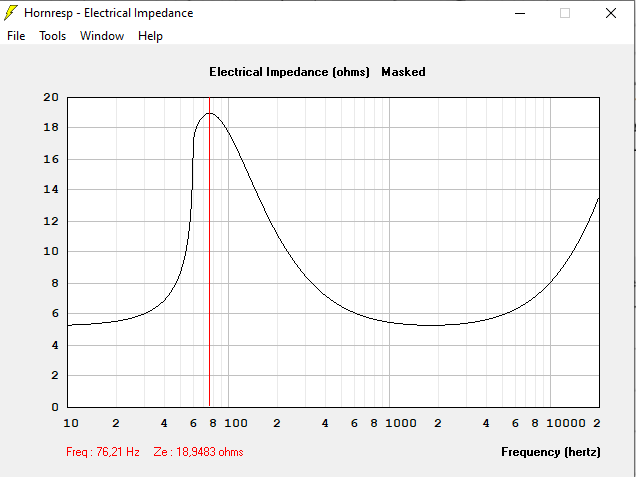
Avec Volume clos = 78 L 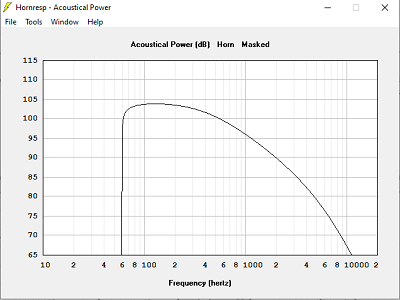
Avec Volume clos = 120 L 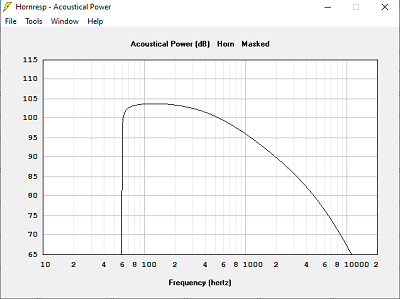
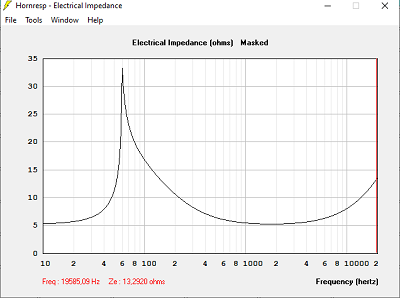
Avec Volume clos = 240 L 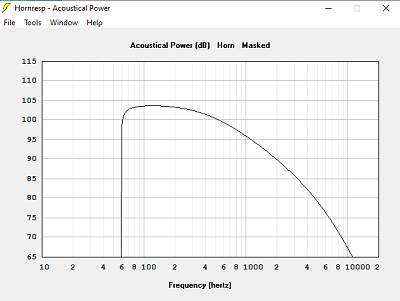
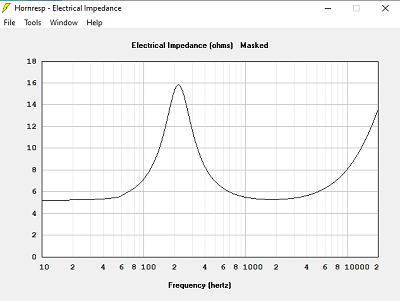
Quand le volume est trop petit, la bande passante est limitée dans le grave.
Quand le volume est trop grand, la courbe d'impédance devient très pointue, et de valeur très élevée : 120 Ohms dans 240 L, 16 Ohms dans 15 L, 19 Ohms dans 78 L.
La bonne solution n'est-elle pas celle qui donne l'impédance électrique calculée identique à l'impédance à vide des haut-parleurs ? Volume clos = 78 L dans notre exemple.
Seule la simulation avec Hornresp pourra vous donner le volume, les mêmes haut-parleur dans une enceinte close de 78 L ont une Fc à 112 Hz. On oublie au plus vite le calcul en enceinte close !!!
Liens :
- Design of a front loaded exponential horn by Martin J. KING.
- Le site de John Inlow sur les pavillons de toutes sortes.
- Pavillon aspect théorique, un peu de théorie.
Une aide au calcul :
Un tableur : Calcul d'un pavillon, 1/4 à 4/4 vous aidera dans les calculs si vous partez d'un haut-parleur.
Calcul d'une loi d'expansion :
Fréquence de calcul de la loi d'expansion : 100.0 Hz, M = 3.6561 m-1, T = 0.707, C = 343.707 m/s.
Fréquence minimale d'utilisation : 150.0 Hz pour le calcul du couple de valeurs (longueur, surface) pour N = 1, 2, 4 et 8.
COMMUN, LOI D'EXPANSION
Surfaces à respecter quelque soit le type de surfaces : Plane, Cylindrique, Sphérique, JMLC, Temporelle ou Tractrix.ROND
surfaces planesRECTANGULAIRE
surfaces planes
Rapport L/H Gorge = 1
Rapport L/H Bouche = 1.5RECTANGULAIRE
surfaces planes
Hauteur constanteN° Longueur
sur l'axeSurface N à 150.0 Hz Diamètre Largeur
1
secteurLargeur
1
secteursHauteur Largeur
1
secteurLargeur
1
secteursHauteur 0 0.00 cm 150.0000 cm2 138.20 mm 122.47 cm 122.474 mm 12.25 cm 33.333 cm 33.333 cm 45.0 cm 1 5.00 cm 171.3796 cm2 147.72 mm 105.41 cm 105.415 mm 16.26 cm 38.084 cm 38.084 cm 45.0 cm 2 10.00 cm 197.2453 cm2 158.47 mm 97.32 cm 97.319 mm 20.27 cm 43.832 cm 43.832 cm 45.0 cm 3 15.00 cm 228.4639 cm2 170.55 mm 94.10 cm 94.103 mm 24.28 cm 50.770 cm 50.770 cm 45.0 cm 4 20.00 cm 266.0816 cm2 184.06 mm 94.06 cm 94.061 mm 28.29 cm 59.129 cm 59.129 cm 45.0 cm 5 25.00 cm 311.3590 cm2 199.11 mm 96.40 cm 96.401 mm 32.30 cm 69.191 cm 69.191 cm 45.0 cm 6 30.00 cm 365.8135 cm2 215.82 mm 100.75 cm 100.751 mm 36.31 cm 81.292 cm 81.292 cm 45.0 cm 7 35.00 cm 431.2697 cm2 234.33 mm 106.96 cm 106.965 mm 40.32 cm 95.838 cm 95.838 cm 45.0 cm 8 40.00 cm 509.9214 cm2 254.80 mm 115.03 cm 115.031 mm 44.33 cm 113.316 cm 113.316 cm 45.0 cm 40.72 cm 522.4830 cm2 N = 8
Posé au sol
+ 2 murs proches257.92 mm 116.35 cm 116.349 mm 44.91 cm 116.107 cm 116.107 cm 45.0 cm 9 45.00 cm 604.4041 cm2 277.41 mm 125.03 cm 125.034 mm 48.34 cm 134.312 cm 134.312 cm 45.0 cm 10 50.00 cm 717.8842 cm2 302.33 mm 137.13 cm 137.133 mm 52.35 cm 159.530 cm 159.530 cm 45.0 cm 11 55.00 cm 854.1645 cm2 329.78 mm 151.56 cm 151.556 mm 56.36 cm 189.814 cm 189.814 cm 45.0 cm 12 60.00 cm 1017.8120 cm2 359.99 mm 168.60 cm 168.596 mm 60.37 cm 226.180 cm 226.180 cm 45.0 cm 60.75 cm 1045.0451 cm2 N = 4
Posé au sol
+ 1 mur proche364.77 mm 171.40 cm 171.400 mm 60.97 cm 232.232 cm 232.232 cm 45.0 cm 13 65.00 cm 1214.3107 cm2 393.21 mm 188.62 cm 188.616 mm 64.38 cm 269.847 cm 269.847 cm 45.0 cm 14 70.00 cm 1450.2456 cm2 429.71 mm 212.05 cm 212.055 mm 68.39 cm 322.277 cm 322.277 cm 45.0 cm 15 75.00 cm 1733.5231 cm2 469.81 mm 239.44 cm 239.436 mm 72.40 cm 385.227 cm 385.227 cm 45.0 cm 16 80.00 cm 2073.6362 cm2 513.83 mm 271.38 cm 271.381 mm 76.41 cm 460.808 cm 460.808 cm 45.0 cm 80.22 cm 2090.0770 cm2 N = 2
Posé au sol515.87 mm 272.90 cm 272.902 mm 76.59 cm 464.462 cm 464.462 cm 45.0 cm 17 85.00 cm 2481.9827 cm2 562.15 mm 308.62 cm 308.625 mm 80.42 cm 551.552 cm 551.552 cm 45.0 cm 18 90.00 cm 2972.2468 cm2 615.17 mm 352.03 cm 352.033 mm 84.43 cm 660.499 cm 660.499 cm 45.0 cm 19 95.00 cm 3560.8578 cm2 673.34 mm 402.62 cm 402.625 mm 88.44 cm 791.302 cm 791.302 cm 45.0 cm 99.43 cm 4180.3031 cm2 N = 1
Totalement
dégagé729.56 mm 454.41 cm 454.410 mm 91.99 cm 928.956 cm 928.956 cm 45.0 cm 20 100.00 cm 4267.5410 cm2 Trop grand 737.13 mm 461.60 cm 461.599 mm 92.45 cm 948.342 cm 948.342 cm 45.0 cm 21 105.00 cm 5115.9782 cm2 Trop grand 807.09 mm 530.36 cm 530.365 mm 96.46 cm 1136.884 cm 1136.884 cm 45.0 cm 22 110.00 cm 6134.6018 cm2 Trop grand 883.79 mm 610.58 cm 610.580 mm 100.47 cm 1363.245 cm 1363.245 cm 45.0 cm 23 115.00 cm 7357.5472 cm2 Trop grand 967.88 mm 704.19 cm 704.194 mm 104.48 cm 1635.010 cm 1635.010 cm 45.0 cm 24 120.00 cm 8825.7970 cm2 Trop grand 1060.06 mm 813.50 cm 813.497 mm 108.49 cm 1961.288 cm 1961.288 cm 45.0 cm 25 125.00 cm 10588.5542 cm2 Trop grand 1161.11 mm 941.19 cm 941.186 mm 112.50 cm 2353.012 cm 2353.012 cm 45.0 cm 26 130.00 cm 12704.8912 cm2 Trop grand 1271.86 mm 1090.43 cm 1090.432 mm 116.51 cm 2823.309 cm 2823.309 cm 45.0 cm 27 135.00 cm 15245.7294 cm2 Trop grand 1393.25 mm 1264.97 cm 1264.968 mm 120.52 cm 3387.940 cm 3387.940 cm 45.0 cm 28 140.00 cm 18296.2157 cm2 Trop grand 1526.29 mm 1469.19 cm 1469.188 mm 124.53 cm 4065.826 cm 4065.826 cm 45.0 cm 29 145.00 cm 21958.5760 cm2 Trop grand 1672.08 mm 1708.27 cm 1708.266 mm 128.54 cm 4879.684 cm 4879.684 cm 45.0 cm 30 150.00 cm 26355.5412 cm2 Trop grand 1831.85 mm 1988.30 cm 1988.299 mm 132.55 cm 5856.787 cm 5856.787 cm 45.0 cm
Un grand merci pour votre visite. --- Retour direct en haut de la page ---

Un grand-père facétieux disait à ses petits enfants que le grand truc blanc tout en haut du Puy-de-Dôme était un thermomètre géant : Quand il deviendra tout rouge il faudra vite se sauver, parce que le volcan va se réveiller !!!
Dôme Acoustique
Contrôle de validation W3C du code HTML 5 de la page, copiez l'adresse de la page avant de cliquer sur le lien.
Contrôle de validation W3C des CSS de la page, copiez l'adresse de la page avant de cliquer sur le lien.
Ce sont deux outils de contrôle pour le webmaster du site Dôme Acoustique, c'est inutile pour les utilisateurs.
Avoir le lien dans chaque page est plus simple pour les retrouver.